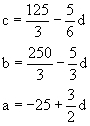zu Aufgabe 1:
Nach Eingabe des (überbestimmten) LGS als 4x4-Matrix [C] und
Bearbeitung durch rref([C]) erhält man nebenstehende diagonalisiert
Matrix.
Aus ihr sind als Informationen zu entnehmen:
- Eine
der vier Gleichungen ist linear abhängig zu einer weiteren,
da eine Nullzeile entstanden ist.
- Das zugehörige LGS
hat dennoch keine Lösung, da eine 0=1 - Zeile entstanden ist.
Antwort: Bei der Angabe zu mindestens einem Monat hat der
Geschäftsführer falsche Angaben gemacht.
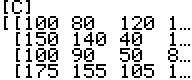
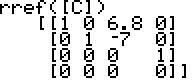
zu Aufgabe 2:
Die
Gesamtmenge von 100kg soll zusammengesetzt sein aus den verschiedenen
Mehlmischungen. Seien a, b, c, d die notwendigen Mengen dieser Mischungen
A, B, C und D. Also gilt a+b+c+d=100 als erste Gleichung. (Da sie
aber auch aus der Addition der drei späteren Gleichungen folgt,
ist die von ihnen linear abhängig und damit überflüssig).
Der Roggenanteil soll 45% betragen, also 45kg der Gesamtmenge. Hier
liefern die einzelnen Mehlmischungen: 0,2a+0,4b+0,4c+0,7d=45. Gleiches
gilt für den Weizenanteil und die restlichen 10kg der Gesamtmenge:
0,7a+0,55b+0,4c+0,2d=45 (Weizen) und 0,1a+0,05b+0,2c+0,1d=10 (Rest).
Dieses LGS wird wieder als Matrix eingegeben und umgeformt
(Koeffizienten zusätzlich als Bruchzahlen).
Wegen der
entstandenen Nullzeile ist das zugehörige LGS unterbestimmt
und universell lösbar.
Wegen der Bestimmungsgleichung
von a wird klar, dass die Mehlmischung D nicht entbehrlich ist:
Es muss von Mischung D mindestens d=50/3 verwendet werden (sonst
wäre a von negativem Wert), aber höchstens d=50 (sonst
wäre c negativ).
Für d=16,667kg folgen c=250/9, also
27,778kg und b=500/9, also 55,555kg - Mischung A würde nicht
benötigt. Für d=50 würden a=50 und b=0 und c=0 folgen,
die Mischungen B und C würden nicht benötigt.
Antwort:
Der Bäcker kann auf mindestens eine der Mehlmischungen A, B
oder C verzichten, und trotzdem wird die beauftragte Geschmacksrichtung
durch die übrigen Mehlmischungen erreicht. Er sollte den Auftrag
annehmen.

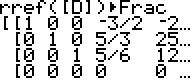
also