Einführung:
Hans betritt
eine Höhle, die von Ratten und Spinnen bewohnt wird. 84 Augen
starren ihn an, und mit 204 Beinen suchen alle Tiere das Weite.
Wieviele Ratten und Spinnen (mit acht Beinen!) sind in der Höhle?
Das Problem soll auf drei Arten gelöst werden: experimentell
geometrisch durch Betrachtung der zugehörigen Geraden, algebraisch
durch Umwandlung einer Matrix in die erweiterte Einheitsmatrix und
algebraisch durch Lösen eines Gleichungssystems.
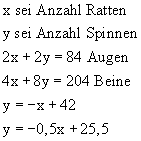
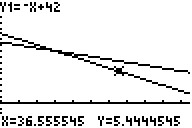
1.) experimentelle Schnittstellenbestimmung
am Graphen
Wir stellen zu beiden Aussagen Gleichungen auf und
lösen diese nach y auf.
Die Terme werden als Funktionen
Y1 und Y2 eingegeben. Die Anzeige muss so eingestellt werden, dass
der Schnittpunkt gut erkennbar ist. Wir führen einen Beobachtungspunkt
entlang eines der Graphen und notieren die ungefähren Koordinaten
des Schnittpunktes, dann verlassen wir die Graphenanzeige.
Tipps: Bildausschnitt ändern mit [ZOOM],[WINDOW];
Im Trace-Modus
wird mit den Cursortasten [Auf][Ab] der Graph gewechselt, mit [<][>]
der Punkt auf dem Graph bewegt.
2.) algebraische Bestimmung der
Lösungskomponenten mittels Matrix
Die Koeffizienten der
beiden Ausgangsgleichungen (Augen und Beine) sollen in einer 2x3-Matrix
eingetragen und die Matrix umgeformt werden.
Nach [II.MATRIX]
[>] [>] 1 wird zuerst die Dimension der Matrix (2x3) eingegeben,
dann folgen die Koeffizienten der beiden Ausgangsgleichungen, jeweils
mit [ENTER] bestätigt. Mit [II.QUIT] wird der Matrixeditor
wieder verlassen.
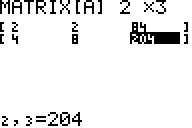
Mit [II.MATRIX] [>] [III.B] wird
im Matrix-Math-Menü die Funktion B:rref() aufgerufen. Sie wandelt
eine erweiterte Matrix um in eine erweiterte Einheitsmatrix. Als
Argument (Parameter) wird rref() die Matrix A übergeben: [II.MATRIX]
1 [ENTER] führt sogleich die Umformung aus.
Es wird die
erweiterte Einheitsmatrix angezeigt. Ihr entnehmen wir die beiden
Gleichungen 1x + 0y = 33 (also x = 33) und 0x + 1y = 9 (also y =
9).
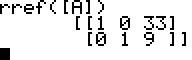
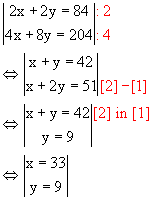
3.) algebraisches Lösen
eines Linearen Gleichungssystems
Beide Gleichungen werden als
Gleichungssystem aufgestellt.
Zuerst werden beide Gleichungen
so dividiert, dass jeweils der Summand x entsteht.
Dann subtrahiert
man die erste von der zweiten Gleichung, tauscht das Ergebnis mit
der zweiten - der weniger bequemen - Gleichung aus.
Schließlich
wird in der Rückeinsetzung das erste Ergebnis y=9 in die erste
Gleichung eingesetzt, wir erhalten auch das zweite Ergebnis x=33.
Aufgabe:
Franz
kommt mit Körnerfutter in das Hühnerhaus, in dem Mäuse
und Hühner wohnen. 234 hungrige Augen schauen ihn an, und mit
268 Beinen stürzen alle zum Futtertrog. Wie viele Hühner,
wie viele Mäuse werden hier gefüttert? Lösen Sie
auch dieses Problem wie oben auf drei Arten. Notieren Sie neu Gelerntes
im Protokollheft. Üben Sie auch mit weiteren
Gleichungssystemen.