Einführung:
Nur mit
Kenntnis einiger Graphenpunkte und Vorgabe des Polynomgrades sollen
mögliche Funktionsgleichungen ermittelt werden, deren Graph
durch die Vorgabepunkte verläuft.
Beispiel:
Der Graph
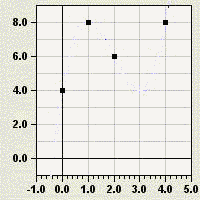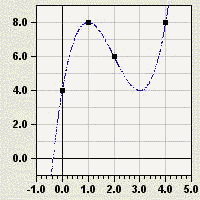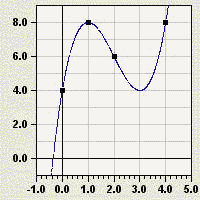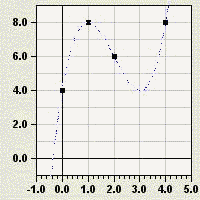
einer Funktion 3. Grades soll durch die Punkte P(1/8), Q(2/6), R(4/8)
und S(0/4) verlaufen.
Lösungsidee:
Durch Einsetzen der Punktkoordinaten
in die allgemeine Funktionsgleichung entstehen vier Gleichungen
mit vier Parametern, die gemeinsam gelten müssen. Dies führt
auf ein Lineares Gleichungssystem. Die resultierende Lösung
beschreibt den Term des nebenstehend dargestellten Graphen.
Aufgabe (zu den weiteren
Teilaufgaben):
a) Wie lautet die allgemeine Gleichung
einer Polynomfunktion dritten Grades?
b) Wieviele Lösungen wird das Lineare Gleichungssystem (LGS) haben?
c) Formulieren Sie die vier funktionalen Bedingungen und formen Sie diese zu vier Bestimmungsgleichungen eines LGS mit den Variablen a,b,c,d um.
d) Stellen Sie das LGS nun als Matrix im GTR auf und lösen Sie es. Interpretieren Sie die Ergebnismatrix und notieren Sie die resultierende Funktionsgleichung.
Lösen eines LGS mittels Einheitsmatrix: siehe hierzu diese Einführungsaufgabe
e) Geben Sie den resultierenden Funktionsterm im Y-Editor ein und betrachten Sie den Graph. Erfüllt er alle Bedingungen, liegen also alle geforderten Punkte auf dem Graph? Prüfen Sie dies auch anhand der Wertetabelle der Funktion.
Wertetabelle konfigurieren:
[II.TBLSET]
Wertetabelle anzeigen:
[II.TABLE]
f) Ermitteln Sie auch die Koordinaten
des Hoch- und des Tiefpunktes
- (1) probeweise im Trace-Modus
- (2) näherungsweise mittels der Funktionen maximum() und minimum():
Hierzu müssen Sie die linke und rechte Bereichsgrenze durch
Eingabe der x-Koordinate oder Bewegen des Punktes mit Cursortasten
und einen Schätzwert (z. B. angebotene rechte Grenze mit [Enter]
übernehmen) angeben.
Probieren Sie hierzu insbesondere
auch 0 als linke und 5 als rechte Grenze. Weshalb sind dies ungeeignete
Bereichsgrenzen? Benennen Sie günstige Grenzen für die
Ermittlung von Hochpunkt und Tiefpunkt.
Hoch- bzw. Tiefpunkt finden:
[II.CALC]
4 bzw. 3
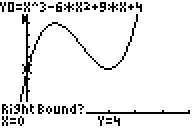
g) Wird der Punkt S(0/4) nicht vorgegeben, entsteht ein unterbestimmtes LGS. Notieren Sie dieses als Matrix B (Tipp: Matrix A als B speichern, Dimension von B ändern) und lösen Sie es mittels rref(). Interpretieren Sie die Ergebnismatrix, notieren Sie daraus alle möglichen Funktionsgleichungen und kontrollieren Sie, ob auch die in d) gefundene Funktion zu dieser sogenannten Funktionenschar gehört.
Matrix A als B speichern: [II.Matrix]
[Enter] [STO>] [II.Matrix]2[Enter] [Enter]
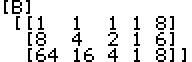
Weitere Teilaufgaben oder zur Lösung (aber zuerst selbst rechnen!)