Lösung der Teilaufgaben a - f):
zu a) Allgemeine Funktionsgleichung
3. Grades:
f(x) = ax³ + bx² + cx + d (mit reellen
Zahlen a,b,c,d)
zu b) Vorüberlegung zur Lösbarkeit des aufzustellenden Gleichungssystems:
Für vier Parameter a,b,c,d gibt es vier Bedingungen (Punkte
des Graphen). Das Lineare Gleichungssystem LGS kann also eindeutig
lösbar sein. Falls aber zwei der Gleichungen zueinander Vielfache
sind (Bsp: a+b=2 und 3a+3b=6), entsteht durch Umformung eine Ergebnisgleichung
0=0 (oder in der zugehörigen Matrix eine Nullzeile). Dann ist
das LGS universell lösbar - es hat unendlich viele Lösungen.
Hier ist eine Musterlösung
dazu.
Andererseits hat das LGS keine Lösung, falls sich
mindestens zwei der vier Gleichungen widersprechen (Bsp: a+b=2
und a+b=1). Also ist es hier noch nicht vorhersehbar, ob und wie
das LGS lösbar ist.
zu c) Bedingungen und zugehörige
Bestimmungsgleichungen:
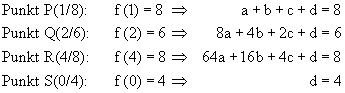
zu d) Zugehörige erweiterte Matrix
und Lösungsmatrix:

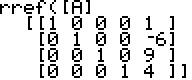
Gleichung der Lösungsfunktion: f(x) = x³
- 6x² + 9x + 4
Lösungsparameter:
a = 1
b = -6
c = 9
d = 4
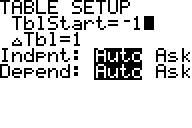
zu e) Tabelleneinstellung und Funktionswertetabelle:
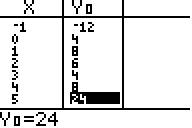
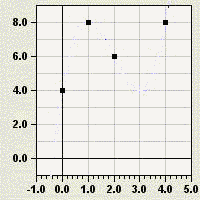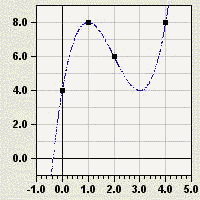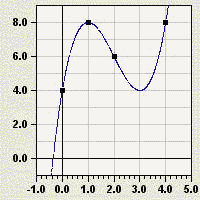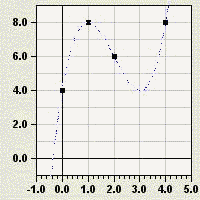
Alle geforderten Punkte liegen tatsächlich auf dem Graph von
f.
Funktionsgraph:
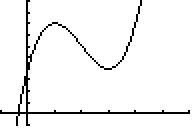
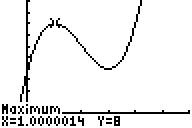
zu f) Koordinaten der Extrempunkte /
günstige Eingaben dazu:
Hochpunkt H(1/8) mit LeftBound
0, RightBound 4, Guess 2;
Tiefpunkt T(3/4) mit LeftBound 2, RightBound 4, Guess 4;
Die ermittelten Ergebnisse enthalten jedoch Rundungsungenauigkeiten!
Bei ungünstiger Wahl der Bereichsgrenzen oder des Schätzwertes
kann es zu unerwarteten Ergebnissen kommen: [II.CALC]4[Enter] mit
LeftBound 0, RightBound 6 und Guess 6 liefert nicht den Hochpunkt,
sondern findet (6/58) als Punkt mit größtem y-Wert im
Bereich.