Aufgabe (Fortsetzung):
Wir
verwenden weiter die zuvor behandelte Aufgabe:
Der Graph einer
Funktion 3. Grades soll durch die Punkte P(1/8), Q(2/6), R(4/8)
und S(0/4) verlaufen.
h) Dieser Aufgabenteil ist recht anspruchsvoll und zeigt eine
interessante Möglichkeit auf, Graphen direkt aus der Matrixlösung
zu zeichnen:
Für eindeutig lösbare Punkte-Funktion-Beziehungen kann
der zugehörige Graph leicht gezeichnet werden:
Speichern
Sie dazu die ermittelte Lösungsmatrix (z. B. als Matrix
F) ab. Die Parameter a,b,c und d des Terms stehen nun in den Matrixzellen
F(1,5) bis F(4,5) und sind z. B. mit [II.RCL][F](1,5) aufrufbar.
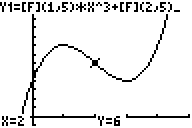 Geben Sie im Y-Editor den in a) notierten allgemeinen
Term ein, ersetzen Sie aber die Parameter a,b,c,d durch die Angabe
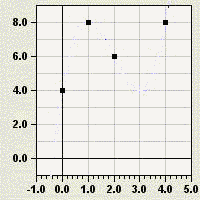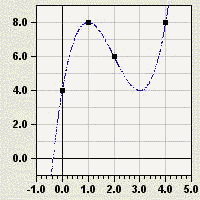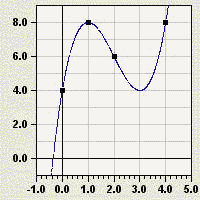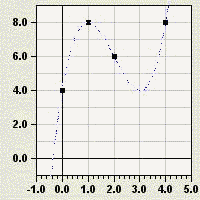
der Matrixzellen. Beim Start des GBS (durch [GRAPH]) wird nun der
Graph mit Komponenten aus der Matrix F gezeichnet. Es sollte dann
(nach geeigneter Window-Einstellung) dieser Graph dargestellt werden.
Geben Sie im Y-Editor den in a) notierten allgemeinen
Term ein, ersetzen Sie aber die Parameter a,b,c,d durch die Angabe
der Matrixzellen. Beim Start des GBS (durch [GRAPH]) wird nun der
Graph mit Komponenten aus der Matrix F gezeichnet. Es sollte dann
(nach geeigneter Window-Einstellung) dieser Graph dargestellt werden.
Kontrollieren Sie mit [TRACE] oder mit [TABLE] alle Vorgabepunkte.
Tipp: Mit (ggf. mehrfachem) [II.ENTRY] holt man frühere Eingaben
zurück und nutzt sie erneut.
 Speichern der Lösungsmatrix:
Speichern der Lösungsmatrix:
![]()
Eingabe des allgemeinen Terms:
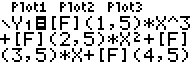
i) Dieser Aufgabenteil
ist sehr anspruchsvoll: Es geht um die Auswirkungen unterbestimmter
LGS bei der Bestimmung von Funktionstermen:
Ändern
Sie nun die Elemente der Matrix A (wiederum in einer Kopie B) so,
als ob der Punkt S(0/4) wie in g) - und in einem weiteren Versuch
statt S der Punkt Q(2/6) - nicht vorgegeben sind. Welche Änderungen
im LGS bzw. in der Matrixkopie B ist hierzu jeweils nötig?
Lösen Sie diese LGS (auch algebraisch!). Interpretieren Sie
die jeweilige Lösungsmatrix und notieren Sie die möglichen
Funktionsgleichungen. Zeigen Sie, dass in einem Fall entsteht:
fd(x) = (1,5 - 0,125d).x³ + (-9,5 + 0,875d).x²
+ (16 - 1,75d).x + d
Zeichnen Sie jeweils den Graph EINER Funktion, indem Sie für
den frei wählbaren Parameter (hier d) einen (bequemen) Wert
auswählen, den speziellen Term - z. B. f0(x) - aufstellen
und diesen im Y-Editor eingeben. ACHTUNG: Die oben in h) behandelte
Methode (Graph zeichnen aus Koeffizientenmatrix F) ist bei unterbestimmten
LGS nicht einfach möglich.
j) Nun soll durch die Punkte P, Q, R und neu durch T(0/5) der Graph einer Funktion dritten Grades gelegt werden. Kann durch ungeschickte Wahl des vierten Punktes keine Lösung entstehen?
k) Es besteht ein Zusammenhang zwischen
der Anzahl vorgegebener Graphenpunkte, dem gewünschten Grad
des Funktionsterms und der Lösbarkeit. Ordnen Sie für
eine Funktion dritten Grades korrekt zu (Mehrfachzuordnung möglich!):
(A) Sind 4 Punkte gegeben, gibt es ...
(B) Mit 5 gegebenen Punkten
gibt es ...
(C) Sind weniger als 4 Punkte gegeben, gibt es ...
(D) Mit nur 2 Vorgabepunkten gibt es ...
(E) Sind 6 Punkte vorgegeben,
gibt es ...
(1) ... keine Lösung.
(2) ...
evtl. eine Lösung.
(3) ... immer eine Lösung.
(4) ... immer viele Lösungen.
(5) ... evtl. viele Lösungen.
(6) ... evtl. keine Lösung.
(7) ... häufig keine Lösung.
Zum Beginn der Aufgabe oder zur Lösung (aber zuerst selbst rechnen!)