Aufgabe:
Weitsprung ist eine der wählbaren Sportarten bei den Bundesjugendspielen.
a) Vor den Bundesjugendspielen trainieren Aline und Beate für den Weitsprung. Ihre heutigen Ergebnisse:
Aline |
3,18m |
3,43m |
3,46m |
3,36m |
3,45m |
|---|---|---|---|---|---|
3,34m |
3,42m |
3,21m |
3,03m |
3,43m |
|
Beate |
3,42m |
3,38m |
3,28m |
3,32m |
3,47m |
3,45m |
3,35m |
3,37m |
3,37m |
3,51m |

a1) Legen Sie zwei Listen ALINE und BEATE an. Stellen Sie die Daten als BoxPlots dar. Geben Sie für die gemeinsame Darstellung beider BoxPlots optimale WINDOW-Werte an.
a2) Argumentieren Sie mit Eigenschaften der BoxPlots:
Wer
hat am Wettbewerbstag wohl die größeren Siegchancen?
Geben Sie jeweils alle charakteristischen Größen der
BoxPlots an (Median, erstes und drittes Quartil, kleinster und größter
Wert, Quartilabstand, Spannbreite). Gibt es hinsichtlich der Persentile
P12,5 und P87,5 (die Whiskers im GTR-Typ ModBoxPlot) Ausreißer?
Zeichnen Sie auch beide BoxPlots.
a3) Unterstützen bzw. widerlegen Sie Ihre obige Vermutung,
indem Sie zusätzlich die durchschnittlich erzielten Weiten,
die mittlere quadratische und die Standardabweichung beider miteinander
vergleichen.
Hinweis: Erzeugen Sie hierzu zwei weitere
Hilfslisten ALIQA und BEAQA der quadratischen Abweichungen vom arithmetischen
Mittel. Definieren Sie diese Hilfslisten anfangs im Statistik-Editor.
Achtung: [II.List] MATH 8 liefert mit variance() zwar
eine Varianz (mittl. quadr. Abweichung);
hier wird aber die
Summe aller quadratischen Abstände statt durch n nur durch
(n-1) dividiert!
stdDev() (mit [II.List] MATH 9) bildet ebenso
die Standardabweichung.
Probe: variance(L1) * (dim(L1) -1)
/ dim(L1) liefert den korrekten Wert für die Varianz der Liste
L1.
a4) Erzeugen Sie weitere Listen mit
zufällig erzeugten Werten und bearbeiten Sie auch hiermit obige
Aufgaben:
round ( randNorm (3.35 , 0.15 , 25 ) , 2 ) STO>
L1
speichert in L1 25 auf zwei Dezimale gerundete Werte um 3.35
mit Standardabweichung 0.15.
round() mit
MATH NUM 2
randNorm()
mit
MATH PRB 6
b) Der Tag der Bundesjugendspiele ist nun gekommen. Alle SchülerInnen der Klassen 8a und 8b nehmen am Weitsprung teil. Jede/r springt dreimal, der weiteste Sprung wird gewertet. Rechts sind die erzielten Bestweiten:
b1) Legen Sie drei Listen WEITE (Mittelwert der Weitenklasse),
W8A und W8B an. Stellen Sie die Daten beider Klassen 8a und 8b als
BoxPlots dar. Geben Sie für die gemeinsame Darstellung beider
BoxPlots optimale WINDOW-Werte an und zeichnen Sie beide BoxPlots
untereinander.
Geben Sie jeweils auch alle charakteristischen
Größen der BoxPlots an (Median, erstes und drittes Quartil,
kleinster und größter Wert, Quartilabstand, Spannbreite).
Gibt es hinsichtlich der Persentile P12 und P88 Ausreißer?
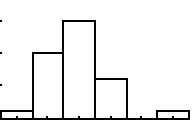 b2) Zu welcher der beiden Klassen gehört
dieses Histogramm?
b2) Zu welcher der beiden Klassen gehört
dieses Histogramm?
Begründen Sie Ihre Antwort durch Zuordnung
von Tabellen- und Histogrammeigenschaften, und zeicnnen Sie auch
das zweite Histogramm.
Hinweis: Zusätzlich wurden
mit xScl=0.2 breitere Werteklassen gebildet; die Stabhöhen
sind durch yScl=5 dargestellt.
b3) Im Wettbewerb aller Klassen gewinnt diejenige mit der durchschnittlich größten Weite und dem dichtesten Leistungsspektrum. Vergleichen Sie jeweils diese beiden Werte; welche Klasse gewinnt?
Weite |
8a |
8b |
|---|---|---|
2,81m - 3,00m |
2 |
1 |
3,01m - 3,10m |
1 |
0 |
3,11m - 3,20m |
4 |
5 |
3,21m - 3,30m |
6 |
5 |
3,31m - 3,40m |
9 |
12 |
3,41m - 3,50m |
4 |
3 |
3,51m - 3,60m |
2 |
4 |
3,61m - 3,70m |
1 |
2 |
3,71m - 3,80m |
0 |
0 |
3,81m - 3,90m |
1 |
0 |
3,91m - 4,00m |
0 |
1 |
4,01m - 4,20m |
0 |
0 |
c) Die Aufgabenstellungen können Sie auch in einer Tabellenkalkulation oder mit dem Programm CellSheet durchführen, das auf dem GTR TI-84 installiert ist. Hierzu gibt Ihnen die Übung 4/2 viele Hilfen.
Eingaben am GTR:
Hinweise:
Neue Liste im Statistik-Editor definieren
und mit zehn Zufallswerten füllen:
STAT EDIT 1 [Enter]
[^] (in Titelzeile) [>] (bis zu freier Namenszelle) (Name eingeben)
[Enter] MATH PRB 1 [Enter] ( 10 ) [Enter]
5 Zufallszahlen mit rand(5):
MATH
PRB 1 [Enter] (5)
Quadratische Abstände der Listenelemente
in L1 vom arithmetischen Mittel als neue Liste QA speichern (LQA
ggf. vorher im Statistik-Editor definieren):
( mean( [II.L1]
) - [II.L1] ) ² [STO>] [II.List] OPS [III.B] [III.Q] [III.A]
[Enter]
Listenname bilden mit
[II.List]
OPS [III.B] (Name)
Standardabweichung der Listenwerte in
L1 mittels Liste QA ermitteln:
Wurzel ( sum (LQA)
/ dim (LQA) ) [Enter]
[II.Wurzel] ( [II.List] MATH
5 [II.List] NAMES (QA auswählen mit Cursor) [Enter] ) : [II.List]
OPS 3 [II.List] NAMES (QA auswählen mit Cursor) [Enter] ) )
[Enter]
Elementsumme mit sum():
[II.List]
MATH 5
Elementanzahl mit dim():
[II.List] OPS 3
25 zufällige, normalverteilte Werte
um Mittelwert 3.35 mit Standardabw. 0.15 auf zwei Dezimale runden
und in Liste L1 speichern:
round ( randNorm (3.35 , 0.15 , 25
) , 2 ) STO> L1 [Enter]
round() mit
MATH NUM 2
randNorm()
mit
MATH PRB 6
BoxPlot mit P12 / P88 - Ausreissern
aus WEITM und W8A:
[II.StatPlot] (wählen)[Enter] (On Type:BoxPlot4
Xlist:WEITM Freq:W8A)
[Window] (2.8<=x<=4 xscl=0.1 -1<=y<=1.5
yscl=1 xres=1) [Graph]