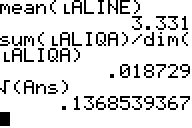Lösung zu Teilaufgabe a):
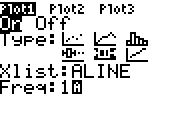
zu a1) Listen im StatistikEditor anlegen, dann BoxPlots definieren, anzeigen und Window geeignet einstellen:

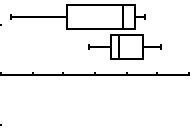
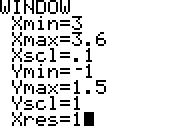
Mittels Trace werden die charakteristischen Werte der BoxPlots ermittelt:
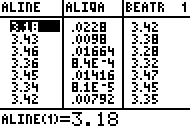
Aline: minX=3,03 Q1=3,21 Median=3,39 Q3=3,43
maxX=3,46
Quartilabstand=3,43-3,21=0,22 Spannbreite=3,46-3,03=0,43
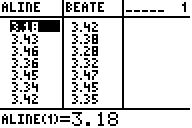
Beate: minX=3,28 Q1=3,35 Median=3,375 Q3=3,45
maxX=3,51
Quartilabstand=3,45-3,35=0,10 Spannbreite=3,51-3,28=0,23
Weder bei Aline noch bei Beate sind Ausreißer festzustellen.
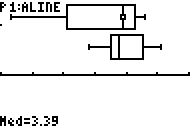
zu a2) Der Median xMA=3,39m von Aline ist größer als der von Beate mit xMB=3,38m, allerdings streut Alines Leistung sehr viel stärker, besonders der untere Quartilbereich ist ausgeprägt. Der obere Quartilbereich liegt bei Beate mit Q3B=3,45m höher als bei Aline mit Q3A=3,43m, Beate erreicht als häufiger bessere Weiten als Aline. Zusammengefasst scheint Beate größere Gewinnchancen zu haben.
zu a3) Hilfslisten ALIQA und BEAQA sind zu erzeugen und arithmetische Mittelwerte und Standardabweichung zu bestimmen:
Aline: arithMittel aM=3,331, also 3,33m Varianz=0,018729,
also 0,02m²
StandAbw s=0,1369, also 0,14m
Beate: arithMittel aM=3,392, also 3,39m Varianz=0,004476,
also 0,00m²
StandAbw s=0,0669, also 0,07m
Im Mittel ist die Leistung von Beate mit aMB=3,39m besser als die von Aline mit aMA=3,33m. Auch schwanken die Leistungen von Beate (mit sB=0,07m) weniger als bei Aline (mit sB=0,14m). Zusammengefasst scheint Beate auch nach dieser Analyse größere Gewinnchancen zu haben.