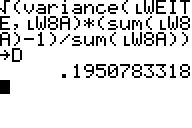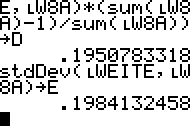Statistik-Übungen in Stufe 11

Lösung zu Teilaufgabe b):

zu b1) Listen im StatistikEditor definieren und anlegen, dann BoxPlots definieren, anzeigen und Window geeignet einstellen:

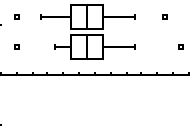
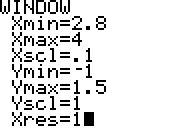
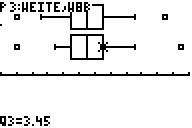
Mittels Trace werden die charakteristischen Werte der BoxPlots ermittelt:

8a: minX=2,90  P12=3,15  Q1=3,25  Median=3,35  Q3=3,45  P88=3,65
maxX=3,95  Quartilabstand=3,45-3,25=0,20  
Spannbreite=3,65-3,15=0,50  Spannweite=3,95-2,90=1,05

8b: minX=2,90  P12=3,05  Q1=3,25  Median=3,35  Q3=3,45  P88=3,65
maxX=3,85  Quartilabstand=3,45-3,25=0,20  
Spannbreite=3,65-3,05=0,60  Spannweite=3,85-2,90=0,95

Sowohl bei der Klasse 8a als auch bei der Klasse 8b gibt es Ausreißer.

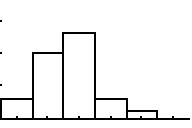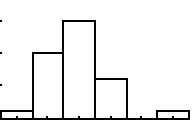
zu b2) Da die Werte zu doppelt breiten Klassen zusammengefasst wurden, ist die höchste Säule und die Lücke vor der weit rechts liegenden Säule signifikant: Die höchste Säule hat die Höhe 15=12+3, links davon ist 10=5+5, rechts davon 6=4+2 zu erkennen. Dann folgen 0=0+0 und 1=1+0. Also gehört das Histogramm (rechts) zur Klasse 8b.

zu b3) Das arithmetische Mittel beider Klassen und die Standardabweichung - hier ohne weitere Hilfslisten durch 'Korrektur' der GTR-errechneten Varianz - werden errechnet:

8a: arithMittel aM=3,317, also 3,32m
   StandAbw s=0,1951, also 0,20m

8b: arithMittel aM=3,361, also 3,36m
   StandAbw s=0,1889996, also 0,19m

Im Mittel ist die Leistung der Klasse 8b mit aM_B=3,36m besser als die der Klasse 8a mit aM_A=3,32m. Auch liegen die Werte mit s_B=0,19m dichter beieinander als in der Klasse 8a mit s_A=0,20m.
Die Klasse 8b gewinnt also den Weitsprungwettbewerb.

Zum Vergleich die korrekt berechnete Standardabweichung - aus der Varianz s²=Summe(quadratische Abstände) / n errechnet - und die mittels stdDev() ermittelte Standardabweichung, die aus der empirischen Varianz (Teilung durch (n-1)) gewonnen wurde. 

Zurück zur Aufgabe