Lösung der Teilaufgaben g h j k):
zu g) Speichern der Matrix A
als Matrix B:
.
Dann letzte Zeile (mit der Bedingung zu Punkt S) ändern
in eine Nullzeile.
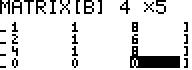
Alternative: Änderung der Matrixdimension (von 4x5 in 3x5) mit [II.Matrix]>>2 ; die letzte Zeile (hier: mit der Bedingung zum Punkt S) fällt dadurch weg.
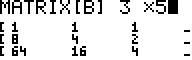
Wir entnehmen der Lösungsmatrix
zu B als Lösungen (mit frei wählbarem d):
a = 1,5
- 0,125d und b = -9,5 + 0,875d und c = 16 - 1,75d und d beliebig
Die zugehörige Funktionenschar fd (da d frei
wählbar) hat die Gleichung
fd(x) = (1,5 - 0,125d).x³
+ (-9,5 + 0,875d).x² + (16 - 1,75d).x
+ d
Mit d = 4 wie in Teil a) ist f4 dann tatsächlich
(wie in Aufgabenteil d gelöst):
f4(x) = (1,5
- 0,5).x³ + (-9,5 + 3,5).x² + (16
- 7).x + 4 = x³ - 6.x² + 9.x
+ 4
Für d=0 wird in Teil i) der Graph behandelt.
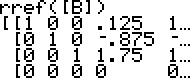(bei geänderter Dimension
fehlt die unterste Nullzeile)
zu h) Der Funktionsterm muss im Y-Editor fehlerfrei eingegeben werden, wie bereits in der Abbildung dargestellt.
zu j) Wieder wird eine Kopie
von A als Matrix B abgespeichert, dort die Zeile zum Punkt S geändert:
von [0 0 0 1 4] in [0 0 0 1 5] für den Punkt T(0/5).
Wir speichern die Lösungsmatrix wieder als F und erhalten aus
ihr:
a = 0,875 und b = -5,125 und c = 7,25 und d = 5 ,
also f(x) = 0,875.x³ - 5,125.x²
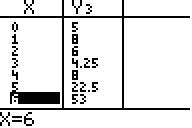
+ 7,25.x + 5 . Graph und (zur Probe) die Wertetabelle
sind rechts abgebildet.
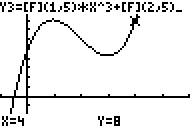
zu k)
(A) Sind 4 Punkte
gegeben, gibt es ... immer eine Lösung.
(wenn keiner
der Punkte genau UNTERHALB eines anderen liegt).
(B) Mit 5 gegebenen
Punkten gibt es ... möglicherweise eine Lösung und machmal
keine Lösung.
(C) Sind weniger als 4 Punkte gegeben, gibt
es ... immer viele Lösungen.
(D) Mit nur 2 Vorgabepunkten
gibt es ... immer viele Lösungen.
(E) Sind 6 Punkte vorgegeben,
gibt es ... häufig keine Lösung.
zu B und E: Probieren Sie es aus: Ergänzen Sie die Matrix um eine weitere Zeile und zwingen Sie den Graph auch durch diesen fünften Punkt. Wann gelingt dies nicht?
Zurück zur Aufgabe oder weiter zur Teillösungen i)