Lösung der Teilaufgabe i):
zu i) Ignorieren des Punktes S ist bereits
oben in der Lösung zu g) behandelt.
Für das Ignorieren
von Punkt Q(2/6) wird in einer Kopie B die zugehörige
Zeile [8 4 2 1 6] zu einer Nullzeile verändert.
Nach Speichern der Lösungsmatrix als F (siehe rechts) lesen
wir aus:
a = -1,25 + 0,25c und b = 5,25 -1,25c und d = 4 und
c beliebig.
Die zugehörige Funktionenschar fc (da c
frei wählbar) hat die Gleichung
fc(x) = (-1,25
+ 0,25c).x³ + (5,25 -1,25c).x² +
c.x + 4 .
EIN Vertreter dieser Schar ist fc=0 mit fc=0(x) = -1,25.x³ + 5,25.x² + 4 , dessen Graph unten abgebildet ist.
Hinweis:
Da als Koeffizienten des Funktionsterms für
das Zeichnen des Graphen nur die Zahlen in der ganz rechten Spalte
verwendet werden - im Y-Editor gaben wir ja [F](1,5)*x^4 ... ein
- werden also verwendet:
a = -1,25 und b = 5,25 und (fehlerhaft,
da in der 3. Zeile aus [F](3,5) ausgelesen - c = 4, obwohl d = 4
korrekt wäre. Also wird gleichzeitig der Anteil von c in den
Parametern a,b als c = 0 verwendet, aber auch c = 4 eingesetzt,
was zum falschen Term fc=0(x)
= -1,25x³ + 5,25x² + 4x führt.
Lösung der bearbeiteten Kopie B
der Matrix A:
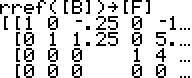
fc=0(x) = -1,25.x³ + 5,25.x² + 4
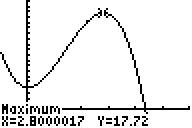
Der rechts gezeigte Graph zu fc=0 (ohne
Punkt Q) ist mit xmin=-1 , xmax=6 , ymin=-1 und ymax=20 (Window-Menü)
dargestellt, zur Kontrolle sind zusätzlich die Hochpunktkoordinaten
(Calc-Menü / maximum) ermittelt worden.
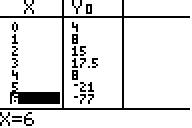
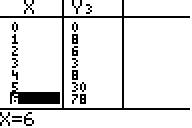
Die Wertetabelle (mit Table) dient der
Probe:
zu fc=0 (ohne Punkt Q) müssen P(1/8),
R(4/8) und S(0/4) auf dem Graph liegen,
fd=0(x) = 1,5.x³ - 9,5.x² + 16.x
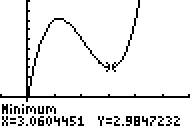
Beim linken Graph zu fd=0 (ohne
Punkt S) sind wiederum nur die in der rechten Zeile stehenden Koeffizienten
berücksichtigt, also (mit d=0) wird verwendet:
fd=0(x)
= 1,5.x³ - 9,5.x² + 16.x
. Auch hier zur Kontrolle die Tiefpunktkoordinaten.
Die Wertetabelle dient der Probe:
zu fd=0 (ohne Punkt S) müssen P(1/8), Q(2/6) und
R(4/8) ablesbar sein.
Tipp: Frühere Eingaben zurückholen mit [II.Entry]!