Abiturklausuren im LK Mathematik der Stufe 13:

Abitur-Übungsklausur 1

3. Aufgabe (Stochastik)

Auf dem Weg von der Wohnung zu seinem Arbeitsplatz hat ein Autofahrer insgesamt 25 Ampeln zu passieren, die unabhängig voneinander geschaltet sind. Erfahrungsgemäß kann er jede Ampel mit einer Wahrscheinlichkeit von 30% ohne Wartezeit passieren. Ansonsten muss er mit einer mittleren Wartezeit von 1 Minute pro Ampel rechnen.

a)  Mit welcher Wahrscheinlichkeit
    a1) zeigt frühestens die 6. Ampel rot?
    a2) erreicht er auf einer Fahrt mehr als die Hälfte der Ampeln bei Grün, kann diese also ohne Verzögerung passieren?

b) Wieviele Ampeln kann er im Mittel bei Grün passieren?
An wievielen Ampeln wird er mit 90%-iger Sicherheit warten müssen? Welche Wartezeiten muss er also einkalkulieren?

c) Im Jahr fährt er 230-mal von der Wohnung zur Arbeitsstätte.
Nun sei die Zufallsvariable W: Wartezeit in Minuten bei 25 Ampeln und 230 Fahrten betrachtet.
Mit welcher Jahres-Wartezeit muss er mit mindestens 90%-iger Sicherheit rechnen?
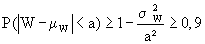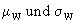Hinweise: Bestimmen Sie hierfür mit der Tschebyschew-Ungleichung den Radius a des gesuchten Intervalls I, und geben Sie abschließend auch I an. Die Ungleichung ist nicht herzuleiten, sind hier Erwartungswert und Standardabweichung dieser Zufallsgröße W.

d) Eine umfangreiche Auswertung der Fahrzeiten von der Wohnung zur Arbeitsstätte hat ergeben, dass die Zufallsgröße T:Fahrzeit in Minuten binomialverteilt ist mit Erwartungswert 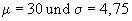(Minuten). Als übliche Fahrt soll eine Fahrt gelten, wenn die Fahrzeit um höchstens 6 Minuten vom Erwartungswert abweicht.
d1) Mit welcher Wahrscheinlichkeit ist dann eine beliebig herausgegriffene Fahrt als übliche Fahrt zu bezeichnen?
d2) Welche Fahrzeit t₀ muss der Autofahrer ansetzen, damit die Wahrscheinlichkeit für eine Fahrzeit, die länger als t₀ ist, höchstens 1/230 beträgt, er also im Mittel pro Jahr höchstens einmal zu spät zur Arbeit kommt?
Hinweis: Berechnen Sie dies jeweils näherungsweise.

e) Nehmen Sie die Wahrscheinlichkeit für eine übliche Fahrt nun mit 0,858 an. Ein Nachbar, der täglich die gleiche Strecke fahren muss, behauptet, jährlich an 210 von 230 Tagen eine übliche Fahrt erlebt zu haben. Kann er (mit 95%-iger Gewissheit) als Lügner bezeichnet werden?

Lösung (aber zuerst selbst rechnen)