gegeben.a) Untersuchen Sie f bezüglich Symmetrie, Definitionsbereich und Asymptoten, Nullstellen, Extrem- und Wendepunkten (vier Extrempunkte!).
Hinweise: Bilden Sie die Ableitungen mit der durch Termdivision gewonnenen Darstellung von f(x). Zeigen Sie u. a., dass
gilt. Führen Sie die hinreichende
Wendepunkt-Überprüfung mittels Vorzeichentabelle durch, beachten Sie
dabei die Polstellen. Nutzen Sie die Symmetrieeigenschaft des Graphen zur Reduzierung
des Rechenaufwandes.b) Zeichnen Sie den Graphen und die Asymptoten in ein Koordinatensystem.
c) Die Normale zur Wendetangente im Ursprung schneidet G(f). Bestimmen Sie die Koordinaten der Schnittpunkte.
d) Zeigen Sie, dass
ein möglicher Term der Stammfunktion ist.Verwenden Sie zum Nachweis ggf. die Integration durch Substitution.
e) Bestimmen Sie das Gesamtmaß aller Flächen, die von G(f) und der ersten Achse vollständig berandet werden (genauer und gerundeter Wert!).
Hinweis: Eine mögliche Zwischenlösung ist hier
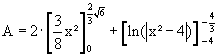. Weshalb ändern sich teilweise die Grenzen? Wie lautet der Term u = g(x) = ... ?