Zur Bearbeitung der Teilaufgabe
a3) mit den Daten von Beate wird einfach der Zellbereich A1:C13
kopiert und im Bereich E1:G13 eingefügt:
F5 (Menu) 2 (Edit...)
4 (Bereichswahl...) (Bereich:) A1:C13 Enter Enter F3 (Copy), dann
mit Cursor auf linke obere Zelle des neuen Bereichs; z. B. E1: F4
(Paste) II.Quit zum Verlassen des Einfügemodus.
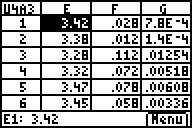
Anschließend müssen noch die zehn Sprungweiten von
Beate in den Zellen E1-E10 eingetragen werden. Alle Berechnungen
erfolgen dann automatisch.
Der Text in Zelle E11 wird mit Enter
II.Alpha " B E A T E eingegeben: II.Alpha schaltet auf Dauer-Alphaeingabe,
Text in Zellen beginnt mit ".
Abschließend kann dieses Tabellenblatt gespeichert werden - z. B. als U4A3 (Übung 4 / Aufgabe a3): F5 (Menu) 1 (Datei...) 2 (Speich. Als...) (Neu:) U4A3 Enter Enter.
Ergebnis: Alines Weiten betrugen im Mittel 3,33m, sie streuten mit der Standardabweichung s = 0,137m. Beates Mittelwert ist 3,39m, die Streuung beträgt s = 0,067m. Beates Leistungen sind also besser und konstanter.
Zur Bearbeitung der Aufgabe
b3) sollte ein neues Tabellenblatt begonnen werden:
F5 (Menu)
2 (Edit...) 3 (Blatt löschen) 2 (Ja)
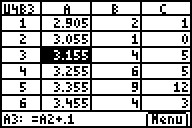
In der Spalte A werden die Weitenklassenmitten eingetragen, in der Spalte B die absoluten Häufigkeiten für die 8a und in Spalte C die der Klasse 8b.
Dazu kann man in den Zellen A3-A11 bequem eine Formel nutzen und kopieren, da die Weitenklassen hier gleich breit sind; nur A1, A2 und A12 enthalten Zahlenwerte.
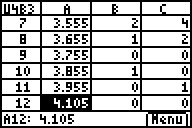
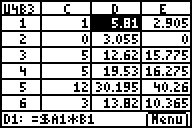Das arithmetische Mittel der
8a- und 8b-Weiten kann hier nicht mittels mean(A1:A12,B1:B12) berechnet
werden. Es muss für 8a in der Hilfsspalte D jede gewichtete
Weitenklassenmitte errechnet werden (in D1: 2,905*2): Formeleintrag
also z. B. in Zelle D1: =$A1*B1. Diese Formel kopieren und in den
Zellen D2-D12 einfügen. Die Hilfsspalte E für die 8b durch
Kopieren der Zelle D1, Einfügen in E1, Kopieren von E1 und
Einfügen in E2-E12 füllen.
Nun kann in den Zellen D14 und E14 das arithmetische Mittel errechnet
werden:
z. B. in D14: =sum(D1:D12)/sum(B1:B12). Es kann nicht
mean() verwendet werden, da die Spaltensumme D durch die Schüleranzahl
der 8a (31) zu teilen ist, nicht durch die Werteanzahl (12).
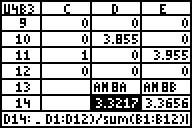
Ähnlich geht man für die Berechnung
der Varianz vor: In zwei Hilfsspalten F und G werden die jeweiligen
quadratischen Abweichungen jeder gewichteten Weitenklassenmitte
vom Mittelwert errechnet;
z. B. in Zelle F1: =($A1-D$14)²*B1
.
Achtung - warum ist die Formel =(($A1-D$14)*B1)² falsch?
Die Formel in F1 kopieren und in F2-F12 einfügen, dann F1 nach G1 einfügen, G1 in G2-G12 einfügen. Die Setzung des $-Zeichens lässt dies korrekt gelingen.
In Zeile 13 sind wieder erläuternde Texte eingegeben, die
Formeln der Zellen F14 und G14 errechnen die Varianz (mittlere quadratische
Abweichung vom Mittelwert) - wieder ohne Verwendung von mean():
z. B. in Zelle F14: =sum(F1:F12)/sum(B1:B12).
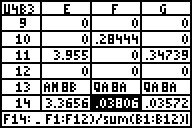
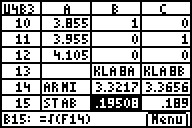
Im Zellenbereich A13:C15 wird nun eine
zusammenfassende Übersicht erstellt: Die Zellen B14 und C14
enthalten einfache Bezüge auf die Zellen D14 und E14 (die arithm.
Mittelwerte; also z. B. B14: =D14).
Die Zellen B15 und C15 errechnen
die Standardabweichung als Wurzel aus den Varianzen in F14 und G14.
Speichern Sie dieses Tabellenblatt zum Beispiel als U4B3 (Übung
4 / Aufgabe b3) ab.
Ergebnis:
Die Klasse 8b erreicht eine größere
mittlere Weite mit 3,37m (statt 3,32m bei 8a). Zusätzlich streuen
die Weiten der 8a mit s=0,189m etwas weniger stark als bei der 8a
mit s=0,195m, Die Klasse 8b gewinnt also.
Tipps zur Arbeit in CellSheet:
- Tabellenblatt speichern: F5 (Menu) 1 (Datei...) 2 (Speich. Als...) (Neu:) U4A3 Enter Enter
- Tabellenblatt öffnen: F5 (Menu) 1 (Datei...) 1 (Öffnen...) (mit Cursor auswählen) Enter
- Tabellenblatt löschen: F5 (Menu) 1 (Datei...) 4 (Löschen...) (mit Cursor auswählen) Enter
- Eingaberichtung ändern (nach rechts statt nach unten): F5 (Menu) 1 (Datei...) 5 (Format...) (Cursor BEWEG) Enter (mit Cursor auf Eingeben) Enter
- Bereich zum Kopieren markieren: F5 (Menu) 2 (Edit...) 4 (Bereichswahl...) (Bereich:) A1:C13 Enter Enter F3 (Copy)
- Kopierten Bereich einfügen: (mit Cursor auf linke obere Zelle des neuen Bereichs; z. B. E1) F4 (Paste) II.Quit
- Automatische
Berechnung an-/ausschalten: F5 (Menu) 1 (Datei...) 5 (Format...)
(AutoBer: J bzw. N wählen) Enter (Eingeben wählen)
Enter
Die Eingaben werden bei 'aus' schneller angenommen, die Neu-Berechnung muss aber jeweils von Hand angestoßen werden: F5 (Menu) 1 (Datei...) 6 (Neuberech.)
