Statistik-Übungen in Stufe 11

Lösung:

zu a)

Bearbeitung mit dem GTR:

ergibt

Häufigkeitsverteilung als Listen L1 und L2 eingeben:
[II.{ ] 1 , 2 , 3 , 4 , 5 , 6 [II. } ] [STO>][II.L1][Enter]
[II.{ ] 3 , 2 , 8 , 11 , 3 , 1 [II. } ] [STO>][II.L2][Enter]
arithmetischen Mittelwert errechnen mittels mean(L1,L2):
[II.List] (Math) 3 [Enter][II.L1] , [II.L2] ) [Enter] 

{ 1  2  3  4  5  6 }
{ 3  2  8  11  3  1 }
mean(L1,L2)
3.42857...

zu b) Der Median ist der mittlere aller (der Größe nach sortierten) Datenelemente. Enthält die Liste eine gerade Anzahl von Elementen, so wird der Median als arithmetisches Mittel der beiden mittleren Elemente ermittelt. Dann ist der Median ggf. mit keinem der Listenelemente identisch!

Als Rohdaten sind hier die 28 Noten gegeben; da dies eine gerade Anzahl ist, gilt für den Median (mit n: Anzahl der Rohdatenelemente):

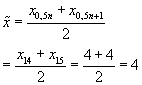
Bearbeitung mit dem GTR:

ergibt

Median der Rohdaten als Median der Verteilung errechnen:
[II.List] (Math) 4 [Enter] [II.L1] , [II.L2] ) [Enter] 

median(L1,L2)
4

Falsch wäre es, nur den Median der Liste L2 zu ermitteln.
Hier würde der Median der (sortierten!) Liste { 1  2  3  3  8  11 } bestimmt.

median(L2)
3

zu c) Wiederum enthält die Rohdatenliste eine gerade Anzahl (26) Elemente:

Bearbeitung mit dem GTR:

ergibt

Korrektur der Anzahl ausreichender Noten im STAT-Listeneditor:
[Stat] 1 (mit Cursor zum Element x₄ der Liste L2) 9 [Enter] [II.Quit]
Median erneut bestimmen:
[II.List] (Math) 4 [Enter] [II.L1] , [II.L2] ) [Enter]

Wert von x₄ der Liste L2
von 11 korrigieren in 9
median(L1,L2)
3.5

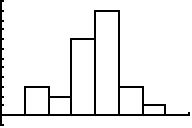
zu d) Statistik-Plotter einrichten für die Listen L1 und L2 (also die Verteilung):
[II.StatPlot] (auswählen) [Enter] (On Type:Histogramm Xlist:L1 Freq:L2)
Window einstellen:
(kleinster und größter Datenwert x sowie vorkommende abs. Häufigkeiten (y) müssen darstellbar sein)
[Window] (0<=x<=8  Xscl=1  -1<=Y<=12 Yscl=1 Xres=1)
Histogramm darstellen: [Graph] 

Zurück zur Aufgabe