Lösung:
zu a) Die Durchschnittsgröße
beträgt
![]()
Die Mannschaft darf in dieser Aufstellung
antreten.
Bearbeitung mit dem GTR:
ergibt
Daten in der Liste L1 speichern:
[II.{ ]1.79 , 1.79 , 1.92 , 1.95 , 1.98 , 2.05 [II. } ] [STO>][II.L1][Enter]
{ 1.79 1.79 1.92 1.95 1.98 2.05 }
arithmetischen Mittelwert mit mean()
errechnen:
[II.List] (Math) 3 [Enter] [II.L1] ) [Enter]
mean(L1)
1.913333...
zu b) x sei die gesucht maximale
Körpergröße.
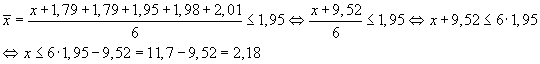
Jeder Ersatzspieler mit einer
Körpergröße von höchstens 2,18m ist einsetzbar.
Bearbeitung mit dem GTR:
ergibt
Summe der Listenelemente ermitteln mit
sum():
[II.List] (Math) 5 [Enter][II.L1] ) [Enter]
Anzahl
der Listenelemente mit dim():
[II.List] (Ops) 3 [Enter][II.L1]
) [Enter]
sum(L1)
11.48
dim(L1)
6
Rechenterm aufstellen: dim(L1) * 1.95
- ( sum(L1) - 1.92) [Enter]
Rechenterm eingeben:
[II.List]
(Ops) 3 [II.L1] ) [x] 1.95 - ( [II.List] (Math) 5 [Enter][II.L1]
) - 1.92 ) [Enter]
dim(L1) * 1.95
- ( sum(L1)
- 1.92) [Enter]
2.18
zu c) Nur eines der Einzeldaten tritt doppelt auf, also besteht das Histogramm nur aus Säulen der Länge 1 und 2.
Bearbeitung mit dem GTR:
ergibt
Statistik-Plotter einrichten für
Liste L1:
[II.StatPlot] (auswählen) [Enter] (On Type:Histogramm
Xlist:L1 Freq:1)
Window einstellen:
(kleinster und größter
Datenwert x sowie vorkommende abs. Häufigkeiten (y) müssen
darstellbar sein):
[Window] (1.78<=x<=2.02 Xscl=0.01 -1<=Y<=3
Yscl=1 Xres=1)
Histogramm darstellen: [Graph]
