Aufgabe 1:
Gesucht sind die durch
die Punkte verlaufenden Parabeln.
a) Stellen Sie jeweils
das Gleichungssystem auf und lösen Sie es.
Notieren Sie
die gesuchte Funktionsgleichung.
b) Geben Sie die erweiterte
Matrix in den GTR ein und lösen Sie sie.
Notieren Sie
die Lösungsmatrix und die gesuchte Funktionsgleichung.
c) Vergleichen Sie jeweils Ihre Lösungen aus a) und b).
(1) P(-1/-3), Q(2/9), R(1/1)
(2) S (0/1), T(2/3), U(2/4)
(3) A(0/2), B(6/-1), C(4/5)
Aufgabe 2:
Die Orte A, B und C liegen
im Koordinatensystem.
a) Wie lang ist von A aus die Strecke
über B nach C [von C aus die Strecke über A nach B] ?
b) Die Fläche zwischen den Orten soll vollständig bebaut
werden. Wie groß ist dieses Bau-Erwartungsland?
(1) A(0/2), B(7/1), C(4/5)
(2) A(0/2), B(6/-1), C(4/5)
Aufgabe 3:
Nennen Sie alle Nullstellen
der Funktionen und beschreiben Sie auch ihre Art.
a) f(x) =
x² + 7x + 10
b) f(x) = x³ - 7x² + 10x
c)
f(x) = 3x³ + 5x² + 12x + 20
d) f(x) = 3x³
+ 12x² + 5x + 20
e) f(x) = (x²+4)(x²+9)
xN=... v xN=...
einfache Nullstelle
doppelte Nullstelle
dreifache Nullstelle
Aufgabe 4:
Geben Sie möglichst
präzise die zugehörige Funktionsgleichung an. Beschreiben
Sie ihre zugrundeliegenden Beobachtungen.
Kontrollieren Sie
Ihre Vermutungen mit dem GTR.
a) 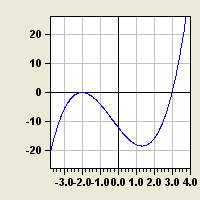 b)
b)  c)
c)

Aufgabe 5:
Der obige Graph aus Aufgabe
4b beschreibt die Anzahl Kunden im Laden ab dem Zeitpunkt t=0 (Ladenöffnung
um 8.00 Uhr). Um welche Uhrzeit musste der Laden wegen einer Bombendrohung
geräumt werden? Wieviele Personen waren ungefähr um 9
Uhr im Laden? Wann befanden sich die meisten Kunden im Laden (wieviele?).
Lösung (aber zuerst selbst rechnen!)