Lösung der Aufgaben 3 - 4:
zu 3a)
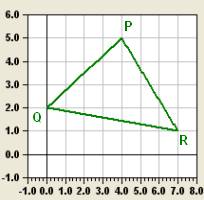
Gegeben sind die Punkte P(4/5),
Q(0/2), R(7/1) , die in ein Koordinatensystem eingetragen und durch
Strecken verbunden werden. Abschließend wird die Dreiecksfläche
(nicht wie hier nur der Rand!) gefärbt.
zu 3b)
Sämtliche Streckenlängen werden mit angelegten
rechtwinkligen (Steigungs-)Dreiecken und dem Satz des Pythagoras
ermittelt:
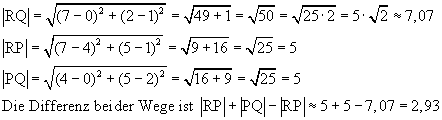
Der Weg über Pasch ist also um ca. 2,93 LE
weiter als der direkte Weg.
Die Dreiecksfläche muss insgesamt
gefärbt sein!
zu 3c)
Geometrische
Begründung: Die Katheten der zugehörigen Steigungsdreiecke
haben die gleiche Länge, wobei die horizontale und die vertikale
vertauscht sind.
Analytische Begründung: Die Steigungen
der beiden Strecken sind reziproke Gegenzahl zueinander, es gilt
also m1 = -1/m2: Konkret sind m1
= mPQ = 3/4 und m2 = mPR = -4/3
.
zu 3d)
Da das Dreieck rechtwinklig ist (siehe c), kann PQ
als Grundseite und PR als Höhe verwendet werden: APQR
= 0,5 |PQ| |PR| = 12,5 .
Das Naturschutzgebiet ist 12,5 FE groß.
zu 4a)
Die zugehörige
Funktion ist vom 3.Grad, da der Graph nur zwei Extrempunkte und
keinen Sattelpunkt sowie vier Nullstellen hat. Der Graph verläuft
von oben nach unten, der Faktor a vor x³ muss also negativ
sein. Zusätzlich muss ungefähr f(0) = 24 gelten.
Ein
erster Termansatz berücksichtigt die doppelte und die einfache
Nullstelle, aufgrund derer die Linearfaktoren festliegen:
f*(x) = a(x + 2)² (x - 3) = a(x² + 4x + 4)(x - 3) =
a(x³ + x² - 8x - 12)
Wegen f(0) = 24 muss also a =
-2 gelten,
somit ist f(x) = -2x³ - 2x² + 16x +24
die gesuchte Funktionsgleichung.
zu 4b)
Analog werden für diese Funktion 4.Grades wieder
die Nullstellen ausgewertet und ein erster Ansatz f*(x) gebildet:
f*(x) = a(x + 1) (x - 2)³ = a(x + 1)(x - 2)(x² - 4x +
4) = a(x² - x - 2)(x² - 4x + 4)
also f*(x) = a(x4
- 5x³ + 6x² + 4x - 8) . Wegen f(0) = -8 muss a = 1 verwendet
werden:
also ist f(x) = x4 - 5x³ + 6x²
+ 4x - 8 die gesuchte Funktionsgleichung.