Lösungen:
zu b)
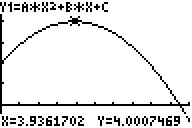
Mit a = -0,13 und b = 1,02
und vorgegebenem c = 2,0 liegt der Zenit bei H (3,92 / 4,00)
und es wird eine Weite von 9,47m erreicht.
Hinweis: Spitzenleistungen
(Weltrekord der Männer: über 23m) erfordern allerdings
andere Bedingungen für den Zenit - die Kugel wird flacher,
aber schneller abgeworfen.
zu c)
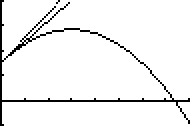
Ein Abwurfwinkel zwischen
40° und 45° erfordert, dass die Kugel in einem vertikalen
Sektor zwischen den Geraden g1 = x + 1,5 (45°)
und g2 = 0,84x + 1,5 (40°) abgeworfen wird.
Dies ergibt sich aus m = tan(alpha). Die Steigungen der
Sektorbegrenzer sind also m1 = tan(45°) = 1
und m2 = tan(40°) = 0,84.
Diese Steigung
hängt in f(x) nur vom Parameter b proportional ab. Dies wird
später durch f'(0) = b gezeigt. Da hier b = 0,9
ermittelt wurde, ist der Abwurfwinkel alpha = arctan(0,9) = 41,99°
- also ein optimaler Abwurfwinkel.
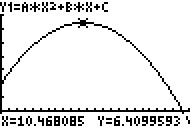
d) Mit einem vorausgesetzten Abwurfwinkel von 40° und einer gewünschten Weite von 23,12m (WR Männer) würde mit b = m = tan(40°) = 0,84 und c = 2,00 hieraus a = -0,042 folgern. Der Zenit läge dann bei H (10,47 / 6,41), die Kugel würde also mit 6,41m sehr hoch fliegen.
Zusatzmaterial:
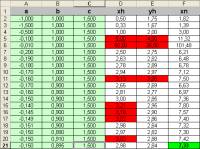
Versuchen Sie selbst, in diesem Excel-Tabellenblatt
für vorgegebene Abwurfhöhen die passenden Parameter und
die zugehörige maximale Weite zu ermitteln.