Einführung:
Beim Kugelstoßen
ähnelt die Kugelflugbahn einer Parabel. Als wichtige Parameter
gehen hier die Anfangshöhe und -geschwindigkeit sowie der Abwurfwinkel
ein. Die Reibung (also der Luftwiderstand) kann wegen des Kugelgewichts
vernachlässigt werden, aber die Erdanziehung spielt eine entscheidende
Rolle.
All dies ist zwar für den Sportler interessant,
aber im Training wird er eher auf Folgendes achten:
- Die maximale
Höhe (der Zenit) der Flugbahn sollte höchstens das Doppelte
der Abwurfhöhe sein - ein steiler Abwurf bringt kürzere
Weiten.
- Dieser Zenit sollte höchstens so weit von der
Abwurfstelle entfernt liegen, wie er hoch liegt - sonst würde
die Kugel - wegen der Erdanziehung - zu früh wieder den Boden
erreichen.

Für die Ermittlung eines geeigneten
Funktionsterms stellen wir fest:
- Zugrunde liegt die allgemeine
Funktionsgleichung quadratischer Funktionen:
f(x) = ax²
+ bx + c .
- Eine der drei Größen a, b, c liegt wegen
der Abwurfhöhe (wir nehmen 1,5m an) sofort fest.
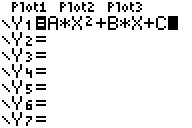
Aufgabe:
a) Geben Sie diesen
allgemeinen Funktionsterm als Y1 ein. Speichern Sie die festliegende
Größe unter gleichem Variablennamen ab. Speichern Sie
auch für die beiden weiteren Parameter erste Startwerte.
Betrachten Sie den resultierenden Funktionsgraph, nachdem Sie die
Anzeige hierzu optimiert haben. Ermitteln Sie den Zenit (die beiden
Hochpunktkoordinaten) und die Wurfweite.
Legen Sie ein Werteprotokoll
an, in das Sie in jeder Zeile die Parameterwerte für a, b,
c , die resultierende Zenithöhe und -weite und die Wurfweite
eintragen.
Verändern Sie nun die gespeicherten Parameterwerte
solange, bis alle obigen Bedingungen für den Wurf erfüllt
sind.
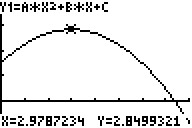
Der optimale Graph sollte etwa nebenstehendes Aussehen
haben. Welche Parameter a, b, c liefern diesen Graph? Wie groß
ist dann die optimale Wurfweite dieses sportlichen Jugendlichen?
Variablen speichern
(z.B. 3,1 als
Variable B):
3.1 [STO>] [III.B] [ENTER]
Zusatzaufgaben:
b) Ein erwachsener
Sportler wirft die Kugel aus einer Höhe von 2,00m. Wie weit
kann er - unter obigen Bedingungen für den Zenit - werfen?
c) Lesen Sie den unten als weiterführende Literatur angebotenen
Aufsatz (insbesondere Kapitel 4). Hier wird u. a. für den Abstoßwinkel
ein optimaler Bereich ermittelt. Muss unter dieser Voraussetzung
die obige Bedingung für die Lage des Wurfzenits verändert
werden? Ist der Abwurfwinkel in der abgebildeten Wurfbahn in diesem
Sinne optimal?
d) Der Weltrekord liegt bei 23,12m mit Abwurfwinkel
40°. Wie lautet hier f(x)?
