Einführung:
Die Nullstellenbestimmung
soll auf drei verschiedene Arten durchgeführt werden, nämlich
experimentell am Graphen, näherungsweise rechnerisch mit dem
GTR-Solver und algebraisch durch Äquivalenzumformung.
Beispiel:
Wir betrachten die quadratische Funktion f mit f(x) = -x² +
5x .
Tipps zur GTR-Eingabe:
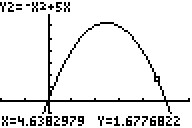1.) experimentelle Nullstellenbestimmung
am Graphen
Geben Sie den Term der Funktion als Y1 ein. Richten
Sie die Anzeige so ein, dass der Graphenverlauf gut sichtbar ist.
Führen Sie einen Beobachtungspunkt entlang des Graphen und
notieren Sie die ungefähren Stellen x, die Nullstellen des
Graphen sind. Verlassen Sie die Graphenanzeige.
Termeingabe mit [Y=],
Anzeige anpassen
mit [ZOOM] und [WINDOW],
Abschreiten des Graphen mit [TRACE],
Ende der Graphenanzeige mit [II.QUIT]
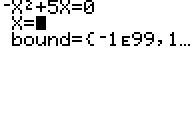2.) näherungsweise
Nullstellenbestimmung mit dem Solver
Geben Sie Term und
Startwert im Solver vor. Wird in der ersten Zeile bereits eine andere
Gleichung gezeigt, muss sie zuvor gelöscht werden.
Geben
Sie hinter eqn:0= den Term der Funktion ein, übernehmen oder
ändern Sie den hinter X= angezeigten Startwert und ggf. den
hinter bound= gezeigten Suchbereich. Hier genügt statt {-1E99
, 1E99} das Intervall {-100 , 100}.
Starten Sie den Solver und
notieren Sie die in der 2. Zeile gezeigte Lösung X=...
Ändern Sie an dieser Stelle den Startwert, um ggf. weitere
Lösungen zu finden und starten Sie den Solver erneut.
Solver vorbereiten mit [MATH] 0, Gleichung
ändern / löschen mit [Auf] und [CLEAR],
Term und
Startwert eingeben,
Solver starten mit [III.SOLVE]
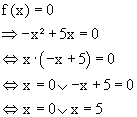3.) algebraische Nullstellenberechnung
mittels Äquivalenzumformungen
Nullstellen-Bedingung:
Funktionswert
ist Null;
Lösen der quadratischen Gleichung durch Ausklammern
und Faktorbetrachtung.
Aufgaben:
a) Kann man bei
den oben beschriebenen Verfahren sicher alle Nullstellen finden?
Wie muss man dazu jeweils vorgehen?
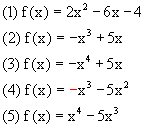b) Ermitteln Sie mit diesen
Verfahren für nebenstehende Funktionen ebenfalls die Nullstellen: