Lösung der Teilaufgabe b):
b) Der Stromverbrauch der Stadt Bärlin
betrug in den Jahren 1995 bis 2000 (in Mrd. kWh):
Jahr |
1995 |
1996 |
1997 |
1998 |
1999 |
2000 |
Verbrauch |
30,7 |
33,1 |
33,7 |
35,3 |
36,8 |
38,0 |
Hinweis:
Einmalig sollte die Einstellung DiagnosticOn
im CATALOG-Menü aktiviert werden, um nach Ermittlung der Regressionsgeraden
nicht nur deren Parameter, sondern zusätzlich auch das Maß
der Korrelation r und den Bestimmtheitsgrad r² ablesen zu können.
zu b1)
Nach Eingabe der Daten in
zwei Listen (z. B. JAHR und VERBR) werden dann mit
STAT CALC
LinReg(aX+b) LJAHR, LVERBR, Y1
die Parameter
der Regressionsgerade so wie die Werte der Korrelation r und des
Bestimmtheitsgrads r² ermittelt: Ca. 98,4% der Daten (also
praktisch alle) werden durch die Regressionsgerade gut dargestellt.
Die Korrelation ist mit fast 0,992 sehr hoch. Eine Prognose erscheint
bei dieser Datengrundlage mittels Linearer Regression sehr sinnvoll.
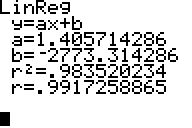
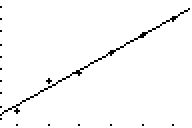
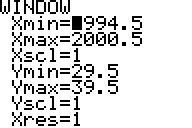Der Graph der Punkt'wolke'
und der Regressionsgeraden kann nach geeigneter WINDOW-Festlegung
(zuvor grob mit ZOOM ZOOMSTAT einrichten) angezeigt werden:
zu b2) Für die Prognose
werden die Parameter der Wertetabelle der angezeigten Funktion Y1
- die Regressionsgerade - zuvor mit [II.TBLSET] eingestellt, dann
die Tabelle mit [II.TABLE] angezeigt:
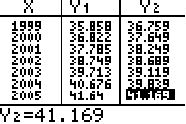
Die Werte für Y1 sind sämtlich theoretische (Prognose-)Daten.
Für das Jahr 2005 kann also ein Verbrauch von ca. 45,143 Mrd kWh angenommen werden.
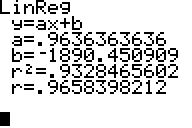zu b3)
Vergleicht
man die tatsächlichen Verbrauchsdaten der Jahre 2001-2004 mit
den prognostizierten, fällt auf, dass sich der tatsächliche
Verbrauch weniger stark als erwartet entwickelte. Deshalb erscheint
es sinnvoll, die Prognose für 2005 nochmals zu überarbeiten
und die tatsächlichen Werte der Jahre 2001-2004 mit einzubeziehen.
Eine erneut ermittelte Regressionsgerade führt nun zum (schlechteren)
Korrelationsgrad r = 0,966 und zum Bestimmtheitsmaß
r² = 93.3%. Die Verbrauchsprognose für das Jahr
2005 sollte also auf 41,64 Mrd kWh korrigiert werden.
Ergänzung:
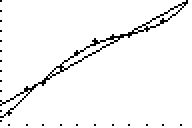
Eine genauere Betrachtung der Punktwolke legt die Vermutung nahe,
dass eine lineare Näherung (Angleichung) zwar möglich,
aber vielleicht nicht optimal ist. Der Versuch, einen höheren
Grad der Regression (nicht 1, sondern z. B. 4) zu wählen, führt
mit
STAT CALC QuartReg LJAHR, LVERBR,
Y2
zu einer weit besseren Anpassung an die festliegenden Punkte.
Es ergibt sich ein Bestimmtheitsgrad von R² = 99,6%
und eine Prognose von 41,169 Mrd kWh für das Jahr 2005. Im
Bild sind sowohl die Regressionsgerade als auch der Regressionsgraph
vierter Ordnung durch die Punktwolke zu sehen.
