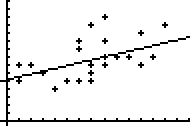
Lösung der Teilaufgabe a):
Hinweis:
Einmalig sollte
die Einstellung DiagnosticOn im CATALOG-Menü aktiviert werden,
um nach Ermittlung der Regressionsgeraden nicht nur deren Parameter,
sondern zusätzlich auch das Maß der Korrelation r und
den Bestimmtheitsgrad r² ablesen zu können.
zu a1)
Nach Eingabe der Daten in
zwei Listen (z. B. E und M) werden dann mit
STAT CALC LinReg(aX+b)
LE, LM, Y1
die Parameter der Regressionsgerade
sowie der Grad r der Korrelation und das Bestimmtheitsmaß
r² ermittelt:
Die Regressionsgerade hat die Gleichung rg(x) = 0,225x + 4,67.
Nur ca. 2,6% der Daten (also praktisch keine) werden durch die Regressionsgerade
gut dargestellt (Bestimmtheitsmaß). Die Korrelation ist mit
r = 0,162 viel zu gering. Es besteht in dieser Gruppe
kein Zusammenhang (also auch kein negativer: je besser in E, desto
schwächer in M) zwischen den Zeugnisnoten in Englisch und Mathematik.
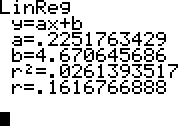
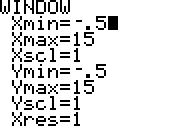Der Graph der Punkt'wolke'
und der Regressionsgeraden kann nach geeigneter WINDOW-Festlegung
(grob mit ZOOM ZOOMSTAT einrichten) angezeigt werden. Mit TRACE
können die einzelnen Punktdaten oder die Gerade mit den Cursortasten
abgetastet werden.
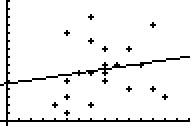
Die (lineare) Abweichung aller Punkte
von der Gerade (in y-Richtung, also für M) kann über die
automatisch erzeugte Residuenliste betrachtet werden:
Hierzu
im STAT-Editor eine neue Liste mit dem Namen RESID anlegen, sofort
werden dort die Abweichungen eingetragen. Hier können
leicht die stärksten Abweichungen nach oben und unten bezogen
auf die Gerade abgelesen werden. Wegen der schwachen Korrelation
sind diese aber bedeutungslos.
zu a2)
(1) Eine starke negative
Korrelation ( -1 < r < -0,4 )
zwischen E- und M-Note besagt: Je besser jemand in Englisch ist,
desto schlechter ist er in Mathematik. Dies ist hier nicht gegeben
(r = 0,162).
(2) Es besteht keinerlei Zusammenhang zwischen erreichter E- und M-Note.
(3) Mit min(LRESID) und max(LRESID) werden die größten Abweichungen aufgefunden, die zugehörigen E-/M-Noten sind (5/1) und (7/13).
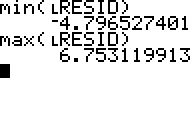
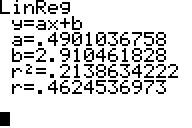zu a3)
Zwischen
D- und M-Noten gibt es eine deutliche Korrelation von r = 0,462.
Bereits 21,4% der Daten (also ca. jedes fünfte Notenpaar) wird
durch die Regressionsgerade gut dargestellt.
Hinweis: In [II.STATPLOT]
als Xlist nun D eintragen!
Die Steigung a=0,49 und der Achsenabschnitt b=2,91 besagen, dass die M-Note fast drei Punkte höher als die D-Note liegt, dies sowohl bei schlechten als auch bei guten Noten, aber eben nur bei ca. 21,4% der Daten.
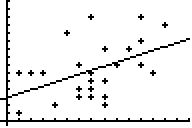
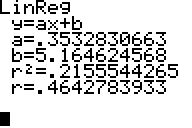Zwischen D- und
E-Noten gibt es eine ähnlich deutliche Korrelation von r = 0,464.
Bereits 21,6% der Daten (also ca. jedes fünfte Notenpaar) wird
durch die Regressionsgerade gut dargestellt.
Hinweis: In [II.STATPLOT]
als Ylist nun E eintragen!
