Vergleichsarbeit Analysis Stufe 11
im 2. Halbjahr des Schuljahres 2000/2001
Vorgesehene Bearbeitungszeit: 2 Unterrichtsstunden
Name:_________________________________________
Kurs:__________________________________________
Aufgabe 1:
Gegeben ist die Funktion f(x) = 0,5x2 – 2x + 1.
- Ermitteln Sie die erste, zweite und dritte Ableitung
von f.
- Berechnen Sie die durchschnittliche Steigung von f im
Intervall [0; 2].
- Welche Steigung hat der Graph von f an der Stelle x =
1 ?
- Stellen Sie die Gleichung der Tangente an den Graphen
von f an der Stelle x = 1 auf.
- In welchem Punkt hat der Graph von f die Steigung – 3
?
- Berechnen Sie mit dem Differenzenquotienten die Ableitung
von f an der Stelle x = 2.
Aufgabe 2:
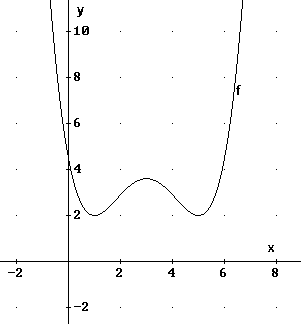
Bild 1
|
Gegeben ist der Graph
der ganzrationalen Funktion f gemäß Bild 1.
- In Bild 2 und Bild 3 sind die Graphen von Ableitungsfunktionen g'1 und g'2 dargestellt. Begründen Sie, warum keine der
beiden Funktionen als Ableitung von f in Frage kommen kann.
- Markieren Sie auf dem Graphen von f in Bild
1 die Anteile in einer anderen Farbe,
für die f '(x)>0 gilt. Skizzieren Sie dann den Graphen von f '(x).
- Skizzieren Sie den Graphen einer Funktion
g1, die als Ableitung die Funktion g'1aus Bild 2 hat.
|
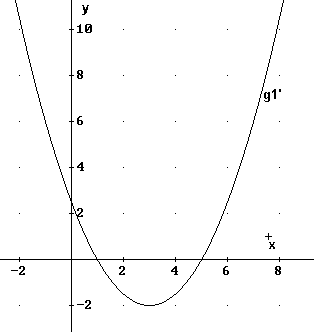
Bild 2
|
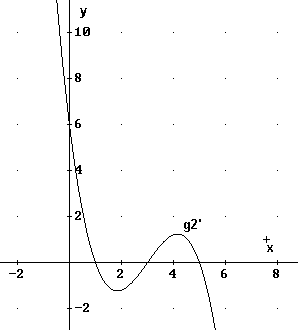
Bild 3
|
Aufgabe 3:
Gegeben sind die Funktionen f(x) = x³ – 8x² + 25x + 14 und g(x) = 20x.
Der Graph von f
ist unten abgebildet.
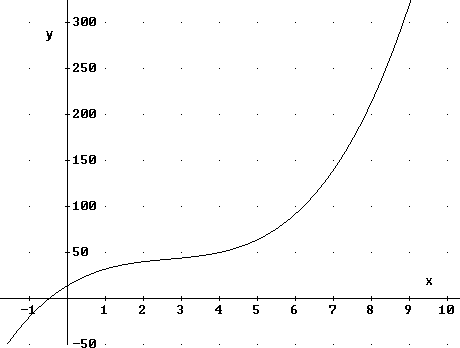
- Weisen Sie rechnerisch nach, dass f keine lokalen Extremstellen hat.
Berechnen Sie die Wendestelle
von f.
- Tragen Sie den Graphen von g in die Zeichnung ein und berechnen Sie die Schnittstellen von
f und g.
- Berechnen Sie die lokalen Extremstellen der Differenzfunktion
d(x) = g(x) – f(x)
= – x³ + 8x² – 5x – 14 .
- Skizzieren Sie mit Hilfe der bisher gewonnenen Ergebnisse
den Graphen der Differenzfunktion d. Benutzen Sie dazu die obige Zeichnung.
Im Rahmen wirtschaftlicher Untersuchungen kann die Funktion
f für x = 0 die "Kostenfunktion"
eines Unternehmens modellieren. Dabei werden die anfallenden Kosten (f(x) Geldeinheiten) in Abhängigkeit
vom produzierten Gut (x Produktionseinheiten) beschrieben. Wird eine Produktionseinheit
für 20 Geldeinheiten verkauft, so stellt g die "Erlösfunktion" dar.
- In welchem Bereich muss die Anzahl x der Produktionseinheiten
liegen, damit das Unternehmen keinen Verlust macht?
Was bedeuten die
Ergebnisse von Aufgabenteil c) in diesem Sachzusammenhang?
Welche Bedeutung
hat hier f(0)?
Quelle: BezReg. Düsseldorf .:. Anpassungen: ©
2004 Ziemke
Letzte Aktualisierung am 2. Januar 2004 durch den WebMaster.
